はじめまして、りょうです。
先日東海オンエアの動画で「ワンパンマンチャレンジ」というものを見かけました。
このチャレンジ、期待値的には何日で終わるのでしょうか?今回はトレーニング友達がいない私が大学数学とプログラミングの力を借りて実際に検証してみました。
大学生時代に一夜漬けをしたマルコフ連鎖による期待値計算も紹介します!
「東海オンエアワンパンマンチャレンジ」とは?
東海オンエアワンパンマンチャレンジとは、ワンパンマンが毎日行っていたトレーニング(ランニング10km、スクワット100回、腹筋100回、腕立て伏せ100回)を5人それぞれのメンバーがメニューのどれか一つを行い、4種類すべてコンプリート出来ていたら1日クリア。3日連続でクリア出来たら企画成功というものでした。
動画内では毎週月~水の3日間それぞれいずれかのメニューを実施して木曜日にメンバー間で答え合わせとしていました。
東海オンエアメンバーは7週目でクリアしておりました。クリアまでの日数が早いとは思いますが、各々ほかのメンバーのメニューを想像したり、曜日によってメニューを固定していたのでチームワークといえます。
さて、これが完全にランダムだったら何週かかるのでしょう。計算してみます。
東海オンエアワンパンマンチャレンジクリアの期待日数
動画のルールにのっとって計算します。
・メンバーは5人
・メニューは4種類
・さぼる日は無いとする
・月-水曜の3日行い木曜にまとめて答え合わせをし、3日連続で成功していた場合クリアとする
4つ目のルールが厄介そうですね。毎日答え合わせしたいところではあります。
1日クリアする確率
1日クリアする場合の数は以下で計算できます。
(1人メニューがかぶる人)×(かぶるメニュー)×(残りの4人のメニュー)×(重複除外)
= 5C1 × 4 × 4! × 1/2
= 240 通り
よって1日クリアする確率はこのようになります
(1日クリアする場合の数)/(1日の全通り)
= 240 / 4^5
= 240 / 1024
= 15 / 64 ≈ 0.234375
23%くらいで1日クリアできるんですね。
3日連続でクリアするまでの期待週数
1日の成功確率を3乗します。
(15 / 64) ^ 3 ≈ 0.0129
一気に1%まで下がってしました。
期待値は逆数を取りますので
(64 / 15) ^ 3 ≈ 77.672
よって完全にランダムでこのチャレンジを行う場合、平均78週間かかる計算になります。ひえぇ。
毎日成功かどうか答え合わせをする場合の期待日数
やはりこれはルール変更の一択です。
動画では、月-水曜の3日行い木曜にまとめて答え合わせをしておりました。
無駄なトレーニング日が増えてしまうので毎日成功かどうかを確認して、失敗だった場合次の日から新たなチャレンジとすることにします。
ということで条件は以下になります。
・メンバーは5人
・メニューは4種類
・さぼる日は無いとする
・毎日答え合わせをし、連続する3日が成功だったらクリアとする
マルコフ連鎖で解く
ここで大学離散数学で登場する「マルコフ連鎖」のお力を借ります。
私は試験のために一夜漬けをするタイプでしたのであまり記憶にありません。これを機に復習します。
Wikipediaからの引用です。
マルコフ連鎖(マルコフれんさ、英: Markov chain)とは、確率過程の一種であるマルコフ過程のうち、とりうる状態が離散的(有限または可算)なもの(離散状態マルコフ過程)をいう。
各時刻において起こる状態変化(遷移または推移)に関して、マルコフ連鎖は遷移確率が過去の状態によらず、現在の状態のみによる系列である。
マルコフ連鎖とは状態遷移がある場合の確率統計などに使われます。
まずは状態遷移図から記述します。
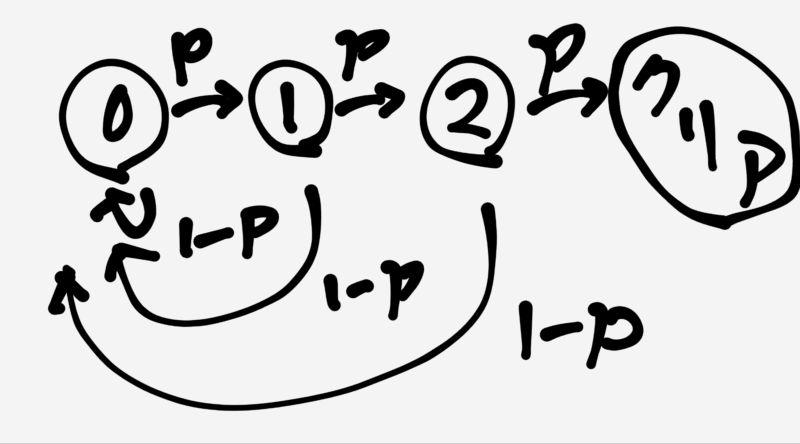
ごめんなさい、ぱぱっと書きました。
状態0,1,2に分けて考えます。
・状態 0: 連続成功日数が0日(最初の状態、または失敗後の状態)
・状態 1: 1日連続で成功した状態
・状態 2: 2日連続で成功した状態
pは1日の成功する確率(15/64)です。
つまり上の図では15/64で成功して次の状態に移行でき、49/64で失敗して最初(状態0)からということが言いたいです。
マルコフ連鎖の期待値計算
状態0からスタートする場合の期待日数をE0とします。
E0 = 1 + p E1 + ( 1 − p ) E0
この式は、1日たったので1プラス、pの確立で状態1に、1-pの確立で状態0に遷移という意味です。
状態1からスタートする場合の期待日数をE1とします。
E1 = 1 + p E2 + ( 1 − p ) E0
状態2からスタートする場合の期待日数をE2とします。
E2 = 1 + p ⋅ 0 + ( 1 − p ) E0 = 1 + ( 1 − p ) E0
これらの式を解いたら以下のようになります(途中式省略)。
E0=(1 + p + p^2 ) / p^3
これにp=15/64を代入すると、
E0 ≈ 99.81
このルールだと平均100日で終わる計算です!
【挑戦中】実際にやってみる
この動画を見ていたら私もワンパンマンチャレンジをやってみたくなります。
ただ、私の周りには共に高めあえるような人は存在しないため仕方なく他メンバのメニュー選びはpythonのプログラムで代用します。
以下が今回使用するコードです。たまたま私とメンバーの1人が共通の「りょう」という名前ですのでりょう以外のメンバーのメニューをランダムで表示します。
import random
menu = ['ランニング', '腕立て伏せ', 'スクワッド', '腹筋']
member = ['てつや', 'としみつ', '虫眼鏡', 'ゆめまる']
for m in member:
print(m+':', random.choice(menu))実行結果は例えば以下のような感じです。
てつや: スクワッド
としみつ: 腕立て伏せ
虫眼鏡: スクワッド
ゆめまる: ランニング
ルールはマルコフ連鎖で解いた以下の通りでいきます。
・メンバーは5人
・メニューは4種類
・さぼる日は無いとする
・毎日答え合わせをし、連続する3日が成功だったらクリアとする
1日目~
・1日目:腕立て伏せ
てつや: 腹筋
としみつ: ランニング
虫眼鏡: スクワッド
ゆめまる: 腹筋
幸先が良すぎる!!早速23%を引きました。
ただ、しんどすぎる。昔ほど体力がないのを身をもって体感しています。
・2日目(1日成功中):ランニング
てつや: 腹筋
としみつ: 腕立て伏せ
虫眼鏡: 腕立て伏せ
ゆめまる: 腕立て伏せ
腕立て伏せ人気過ぎない?
こんなこともあります。
ただ、10kmランがしんどすぎます。
・3日目:休み
てつや: 腕立て伏せ
としみつ: スクワッド
虫眼鏡: スクワッド
ゆめまる: スクワッド
3日目にして休んでます。筋肉痛など重なりさぼりました。
三日坊主も3日続いてるので偉大なことなんですね。
ただ、ほかのチャレンジメンバーが電脳世界の住人なので罪悪感は皆無です。
結果論ですが、私が何をやっても成功にはならなかったのでこれはラッキーです。
・4日目:腕立て伏せ
てつや: 腕立て伏せ
としみつ: ランニング
虫眼鏡: 腹筋
ゆめまる: スクワッド
私がいなくてもクリアできてた珍しい日です。うれしい。
終わりに
現在もひそかに継続中ですので応援いただけますと幸いです。








